本博客日IP超过2000,PV 3000 左右,急需赞助商。
极客时间所有课程通过我的二维码购买后返现24元微信红包,请加博主新的微信号:xttblog2,之前的微信号好友位已满,备注:返现
受密码保护的文章请关注“业余草”公众号,回复关键字“0”获得密码
所有面试题(java、前端、数据库、springboot等)一网打尽,请关注文末小程序
腾讯云】1核2G5M轻量应用服务器50元首年,高性价比,助您轻松上云
通过最近一段时间的试验,我发现周六周日写原创,没多少人看!
因此,以后尽量将周六周日写的原创文章,放在周一和周五之间发布!
Java 程序员需要经常关注一些国外大神级别程序员的动向。比如,我经常关注:Disruptor、Doung Lea、Martin Fowler等等。通过他们的最新文章和言论,我会获得不少的有用信息。
几年前(具体时间忘记了)我 Watch 了 Hystrix,有一天发现,Hystrix 在更新代码中,将 AtomicLong 替换成了 LongAdder。
后来,我才明白 Hystrix 需要根据过去一段时间内失败的请求次数来判断是否打开熔断开关。所以它会维护一个时间窗口,并不断向该窗口中累加失败请求次数,在多线程环境下一般会使用 AtomicLong,但是 Hystrix 中目前是 LongAdder。
我特地查了一下,发现 Hystrix 和 Java8 中的 LongAdder 还有一些细微差别,不过整体思路是一样的,下面的分析都是以 jdk 为准的。
为什么 Hystrix 使用 LongAdder 而不是 AtomicLong 呢?
在 java8 中 LongAdder 的 Java doc 中有以下说明:
❝
This class is usually preferable to AtomicLong when multiple threads update a common sum that is used for purposes such as collecting statistics, not for fine-grained synchronization control. Under low update contention, the two classes have similar characteristics. But under high contention, expected throughput of this class is significantly higher, at the expense of higher space consumption.❞
在存在高度竞争的条件下,LongAdder 的性能会远远好于 AtomicLong,不过会消耗更多空间。高度竞争当然是指在多线程条件下的高并发场景。
我们知道 AtomicLong 是通过 cas 来更新值的,按理说是很快的。但是 LongAdder 为什么会比它更快,是还有其他什么更快的手段吗?先不管这些,直接实验一下,看是不是真的更快。
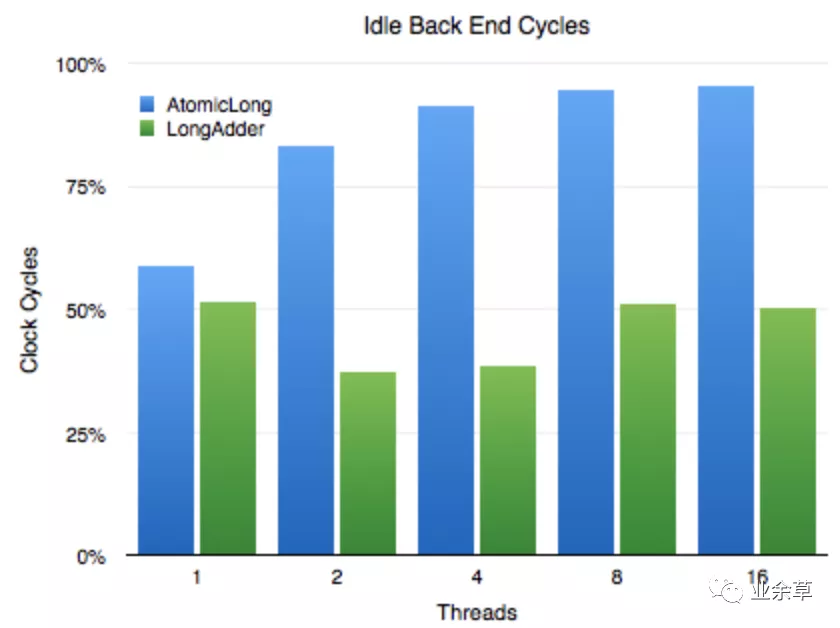
性能对比
AtomicLong、LongAdder、long 的性能测试代码如下所示:
public class TestAtomic {
private static final int TASK_NUM = 1000;
private static final int INCREMENT_PER_TASK = 10000;
private static final int REPEAT = 10;
private static long l = 0;
public static void main(String[] args) throws Exception {
repeatWithStatics(REPEAT, () -> testAtomicLong());
repeatWithStatics(REPEAT, () -> testLongAdder());
repeatWithStatics(REPEAT, () -> testLong());
}
public static void testAtomicLong() {
AtomicLong al = new AtomicLong(0);
execute(TASK_NUM, () -> repeat(INCREMENT_PER_TASK, () -> al.incrementAndGet()));
}
public static void testLong() {
l = 0;
execute(TASK_NUM, () -> repeat(INCREMENT_PER_TASK, () -> l++));
}
public static void testLongAdder() {
LongAdder adder = new LongAdder();
execute(TASK_NUM, () -> repeat(INCREMENT_PER_TASK, () -> adder.add(1)));
}
public static void repeatWithStatics(int n, Runnable runnable) {
long[] elapseds = new long[n];
ntimes(n).forEach(x -> {
long start = System.currentTimeMillis();
runnable.run();
long end = System.currentTimeMillis();
elapseds[x] = end - start;
});
System.out.printf("total: %d, %s\n", Arrays.stream(elapseds).sum(), Arrays.toString(elapseds));
}
private static void execute(int n, Runnable task) {
try {
CountDownLatch latch = new CountDownLatch(n);
ExecutorService service = Executors.newFixedThreadPool(100);
Runnable taskWrapper = () -> {
task.run();
latch.countDown();
};
service.invokeAll(cloneTask(n, taskWrapper));
latch.await();
service.shutdown();
} catch (Exception e) {}
}
private static Collection<Callable<Void>> cloneTask(int n, Runnable task) {
return ntimes(n).mapToObj(x -> new Callable<Void>() {
@Override
public Void call() throws Exception {
task.run();
return null;
}
}).collect(Collectors.toList());
}
private static void repeat(int n, Runnable runnable) {
ntimes(n).forEach(x -> runnable.run());
}
private static IntStream ntimes(int n) {
return IntStream.range(0, n);
}
}上面是用 1000 个并发任务,每个任务对数据累加 10000 次,每个实验测试 10 次。
输出:
total: 1939, [258, 196, 200, 174, 186, 178, 204, 189, 185, 169]
total: 613, [57, 45, 47, 53, 69, 61, 80, 67, 64, 70]
total: 1131, [85, 67, 77, 81, 280, 174, 108, 67, 99, 93]
从上往下依次是 AtomicLong,LongAdder,long。
从结果能看到 LongAdder 确实性能高于 AtomicLong,不过还有一个让我非常吃惊的结果,就是 LongAdder 竟然比直接累加 long 还快(当然直接累加 long 最终得到的结果是错误的,因为没有同步)。这个有些反常识了,其实这里涉及到了一些隐藏的问题,就是 cache 的 false sharing,因为平时编程时不太会关注 cache 这些,所以碰到这个结果会出乎预料,得会再详细的解释。
LongAdder 源码分析
先来分析一下 LongAdder 为什么会比 AtomicLong 快,是不是用到了什么比 cas 还快的东西。
LongAdder 的父类 Striped64 的注释中已经将整个类的设计讲的很清楚的了,类中主要维护两个值,一个 long 型的 base 属性,一个 Cell 数组,它们值的和才是真正的结果。Cell 是对 long 的一个包装,为什么将 long 包装起来,猜测有两个原因:
- 可以在类中添加 padding 数据,避免 false sharing
- 包装起来才好使用 cas。
LongAdder.add 的流程简单描述就是,先尝试通过 cas 修改 base,成功则返回,失败则根据当前线程 hash 值从 Cell 数组中选择一个 Cell,然后向 Cell 中 add 数据。Cell 数组是动态增长的,并且是用时才初始化的,这是为了避免占用过多空间。
看到注释大概能猜到为什么快了,LongAdder 仍然用的 cas,快是因为在高度竞争的条件下,对一个值进行修改,冲突的概率很高,需要不断 cas,导致时间浪费在循环上,如果将一个值拆分为多个值,分散压力,那么性能就会有所提高。
下面来看源码,进入 LongAdder 的 add 方法:
public void add(long x) {
Cell[] as; long b, v; int m; Cell a;
if ((as = cells) != null || !casBase(b = base, b + x)) {
boolean uncontended = true;
if (as == null || (m = as.length - 1) < 0 ||
(a = as[getProbe() & m]) == null ||
!(uncontended = a.cas(v = a.value, v + x)))
longAccumulate(x, null, uncontended);
}
}上面先对 base 进行 cas 操作,然后判断 Cell 数组是否为空,不为空则根据当前线程 probe 值(类似 hash 值)选择 Cell 并进行 cas,都不成功进入 longAccumulate 方法。
final void longAccumulate(long x, LongBinaryOperator fn,
boolean wasUncontended) {
int h;
if ((h = getProbe()) == 0) {
ThreadLocalRandom.current();
h = getProbe();
wasUncontended = true;
}
boolean collide = false;
for (;;) {
Cell[] as; Cell a; int n; long v;
if ((as = cells) != null && (n = as.length) > 0) {// (1)
if ((a = as[(n - 1) & h]) == null) {// (1.1)
if (cellsBusy == 0) {
Cell r = new Cell(x);
if (cellsBusy == 0 && casCellsBusy()) {
boolean created = false;
try {
Cell[] rs; int m, j;
if ((rs = cells) != null &&
(m = rs.length) > 0 &&
rs[j = (m - 1) & h] == null) {
rs[j] = r;
created = true;
}
} finally {
cellsBusy = 0;
}
if (created)
break;
continue;
}
}
collide = false;
}
else if (!wasUncontended)
wasUncontended = true;
else if (a.cas(v = a.value, ((fn == null) ? v + x :
fn.applyAsLong(v, x)))) // (1.2)
break;
else if (n >= NCPU || cells != as)
collide = false;
else if (!collide)
collide = true;
else if (cellsBusy == 0 && casCellsBusy()) {// (1.3)
try {
if (cells == as) {
Cell[] rs = new Cell[n << 1];
for (int i = 0; i < n; ++i)
rs[i] = as[i];
cells = rs;
}
} finally {
cellsBusy = 0;
}
collide = false;
continue;
}
h = advanceProbe(h);
}
else if (cellsBusy == 0 && cells == as && casCellsBusy()) {// (2)
boolean init = false;
try {
if (cells == as) {
Cell[] rs = new Cell[2];
rs[h & 1] = new Cell(x);
cells = rs;
init = true;
}
} finally {
cellsBusy = 0;
}
if (init)
break;
}
else if (casBase(v = base, ((fn == null) ? v + x :
fn.applyAsLong(v, x))))// (3)
break;
}
}Cell 数组不为空时进入分支(1),如果根据当前线程 hash 获得的 Cell 为 null,则进入(1.1)开始实例化该 Cell,否则进入(1.2)对 Cell 进行 cas,不成功的话表示冲突比较多,开始进入(1.3)对 Cell 数组扩容了,cellsBusy 是用 cas 实现的一个 spinlock。
Cell 数组为空且获取到 cellsBusy 时进入分支(2),开始初始化 Cell 数组;
分支(1)和(2)都进不去,没办法,只能再次对 base 进行 cas。
上面只是对源码做了粗略的分析,这些我们都不需要较真去弄的非常清楚,毕竟世界上只有一个 Doug Lea,我们只需要知道 LongAdder 是怎么比 AtomicLong 快的就行,实际就是用多个 long 来分担压力,一群人到十个盘子里夹菜当然比到一个盘子里夹菜冲突小。
实现一个简化版的 LongAdder
知道了原理,那我们就自己来实现一个简陋的 LongAdder。
public class MyLong {
private static final int LEN = 2 << 5;
private AtomicLong[] atomicLongs = new AtomicLong[LEN];
public MyLong() {
for (int i = 0; i < LEN; ++i) {
atomicLongs[i] = new AtomicLong(0);
}
}
public void add(long l) {
atomicLongs[hash(Thread.currentThread()) & (LEN - 1)].addAndGet(l);
}
public void increment() {
add(1);
}
public long get() {
return Arrays.stream(atomicLongs).mapToLong(al -> al.get()).sum();
}
// 从 HashMap 里抄过来的
private static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
}在最上面的 TestAtomic 类中加上方法:
public static void main(String[] args) throws Exception {
repeatWithStatics(REPEAT, () -> testAtomicLong());
repeatWithStatics(REPEAT, () -> testLongAdder());
repeatWithStatics(REPEAT, () -> testLong());
repeatWithStatics(REPEAT, () -> testMyLong());
}
public static void testMyLong() {
MyLong myLong = new MyLong();
execute(TASK_NUM, () -> repeat(INCREMENT_PER_TASK, () -> myLong.increment()));
}输出:
total: 1907, [176, 211, 192, 182, 195, 173, 199, 229, 184, 166]
total: 641, [67, 50, 45, 53, 73, 58, 80, 63, 69, 83]
total: 947, [90, 82, 70, 72, 87, 78, 136, 107, 77, 148]
total: 670, [81, 80, 73, 67, 57, 94, 62, 49, 57, 50]可以看到性能比 AtomicLong 好多了。
为什么 LongAdder 比直接累加 long 还快
前面解释了 LongAdder 比 AtomicLong 快,但是为什么它还会比 long 快?解答这个问题之前要先介绍伪共享的概念。
伪共享(false sharing)
在计算机中寻址是以字节为单位,但是 cache 从内存中复制数据是以行为单位的,一个行会包含多个字节,一般为 64 字节,每个 CPU 有自己的 L1、L2 cache,现在有两个变量x、y 在同一行中,如果 CPU1 修改 x,缓存一致性要求数据修改需要马上反应到其他对应副本上,CPU2 cache 对应行重新刷新,然后 CPU2 才能访问 y,如果 CPU1 一直修改 x,CPU2 一直访问 y,那么 CPU2 得一直等到 cache 刷新后才能访问 y,带来性能下降,产生这个问题的原因有两方面:
- x、y 位于同一行
- 两个 CPU 会频繁的访问这两个数据,如果这两个条件其中一个不成立,那就不会产生问题。更多关于伪共享的概念建议大家自行搜索,或者我后面抽时间写文章。
解决办法
既然这个问题出现了,那肯定是有解决办法的。一般就是添加 padding 数据,来将 x、y 隔开,让它们不会位于同一行中。
Java 中的话,在 Java7 之前需要手动添加 padding 数据,后来JEP 142提案提出应该为程序员提供某种方式来标明哪些字段是会存在缓存竞争的,并且虚拟机能够根据这些标识来避免这些字段位于同一行中,程序员不用再手动填充 padding 数据。
@Contended 就是应 JEP 142 而生的,在字段或类上标准该注解,就表示编译器或虚拟机需要在这些数据周围添加 padding 数据。@Contended 得具体用法,我后面再写相关资料。
下面实验一下来观察 false sharing:
public class TestContended {
private static int NCPU = Runtime.getRuntime().availableProcessors();
private static ForkJoinPool POOL = new ForkJoinPool(NCPU);
private static int INCREMENT_PER_TASK = 1000000;
private static final int REPEAT = 10;
private static long l = 0;
private static long l1 = 0;
private static long l2 = 0;
private static long cl1 = 0;
private static volatile long q0, q1, q2, q3, q4, q5, q6;
private static long cl2 = 0;
public static void main(String[] args) {
repeatWithStatics(REPEAT, () -> testLongWithSingleThread());
repeatWithStatics(REPEAT, () -> testLong());
repeatWithStatics(REPEAT, () -> testTwoLong());
repeatWithStatics(REPEAT, () -> testTwoContendedLong());
}
public static void testLongWithSingleThread() {
repeat(2 * INCREMENT_PER_TASK, () -> l++);
}
public static void testLong() {
asyncExecute2Task(() -> repeat(INCREMENT_PER_TASK, () -> l++), () -> repeat(INCREMENT_PER_TASK, () -> l++));
}
public static void testTwoLong() {
asyncExecute2Task(() -> repeat(INCREMENT_PER_TASK, () -> l1++), () -> repeat(INCREMENT_PER_TASK, () -> l2++));
}
public static void testTwoContendedLong() {
asyncExecute2Task(() -> repeat(INCREMENT_PER_TASK, () -> cl1++), () -> repeat(INCREMENT_PER_TASK, () -> cl2++));
}
public static void repeatWithStatics(int n, Runnable runnable) {
long[] elapseds = new long[n];
ntimes(n).forEach(x -> {
long start = System.currentTimeMillis();
runnable.run();
long end = System.currentTimeMillis();
elapseds[x] = end - start;
});
System.out.printf("total: %d, %s\n", Arrays.stream(elapseds).sum(), Arrays.toString(elapseds));
}
private static void asyncExecute2Task(Runnable task1, Runnable task2) {
try {
CompletableFuture.runAsync(task1, POOL)
.thenCombine(CompletableFuture.runAsync(task2, POOL), (r1, r2) -> 0).get();
} catch (Exception e) {}
}
private static void repeat(int n, Runnable runnable) {
ntimes(n).forEach(x -> runnable.run());
}
private static IntStream ntimes(int n) {
return IntStream.range(0, n);
}
}我这里时手工添加了 padding 数据。目前缓存行大小一般为 64 字节(也可以通过 CPUZ 来查看),也就是填充 7 个 long 就可以将两个 long 型数据隔离在两个缓存行中了。
输出:
total: 16, [9, 5, 1, 0, 0, 0, 0, 1, 0, 0]
total: 232, [35, 35, 33, 24, 25, 23, 13, 15, 15, 14]
total: 148, [17, 15, 14, 16, 14, 15, 13, 17, 12, 15]
total: 94, [8, 8, 8, 8, 15, 9, 10, 11, 8, 9] 从上往下依次为:
- 单线程累加一个 long;
- 两个线程累加一个 long;
- 两个线程累加两个 long,这两个 long 位于同一缓存行中;
- 两个线程累加两个 long,且它们位于不同缓存行中。
从上面的结果看,padding 还是很有效的。结果 2 相比于 1,不仅会有线程切换代价还会有 false sharing 问题,对于纯计算型任务线程个数不要超过 CPU 个数。不过,结果 2 和 3 差距有点大。
我猜测,这个应该是类变量 l1 和 l2 已经不是同一缓存行了。
如果我们在 l2 后再增加一个变量 long l3。testTwoLong 的两个线程方法修改为 l2++,l3++ 就会发现 testLong、testTwoLong 的执行时间差不多一样了远大于 testTwoContendedLong。
参考资料
- LongAdder vs AtomicLong:
http://blog.palominolabs.com/2014/02/10/java-8-performance-improvements-longadder-vs-atomiclong/ - atomic fetch-and-add vs compare-and-swap:
https://blogs.oracle.com/dave/atomic-fetch-and-add-vs-compare-and-swap - False sharing:
https://en.wikipedia.org/wiki/False_sharing - JEP 142: Reduce Cache Contention on Specified Fields:
http://openjdk.java.net/jeps/142

最后,欢迎关注我的个人微信公众号:业余草(yyucao)!可加作者微信号:xttblog2。备注:“1”,添加博主微信拉你进微信群。备注错误不会同意好友申请。再次感谢您的关注!后续有精彩内容会第一时间发给您!原创文章投稿请发送至532009913@qq.com邮箱。商务合作也可添加作者微信进行联系!
本文原文出处:业余草: » 面试官:为什么LongAdder性能比long还快
